OPRO Framework: Optimization by PROmpting
Using Large Language Models as Iterative Black-Box Optimizers
Abstract
This article explores OPRO (Optimization by PROmpting), a novel approach that leverages large language models (LLMs) as black-box optimizers. Rather than using traditional optimization algorithms, OPRO guides LLMs to iteratively generate and improve solutions through natural language prompting. We’ll examine how this framework works, explore practical applications across multiple domains, and provide code examples to demonstrate its implementation.
1. Introduction
Optimization tasks permeate mathematics, engineering, and machine learning—from classical problems like linear regression and the traveling salesman problem to modern challenges such as prompt engineering. Traditionally, these tasks require specialized algorithms—gradient-based or derivative-free optimization methods—that demand formal problem definitions, gradient access, or domain-specific hand-tuning.
OPRO (“Optimization by PROmpting”) offers a fundamentally different approach by using Large Language Models (LLMs) themselves as black-box optimizers. Unlike conventional perspectives of “LLMs as function approximators” or “LLMs as reasoners,” OPRO proposes:
“Given an objective that can be computed for a candidate solution, let an LLM iteratively propose better solutions based on the history of previously scored solutions—simply by describing the optimization loop in natural language prompts.”
In essence, OPRO transforms an optimization problem into a prompting problem—where the language model attempts to improve upon previously generated solutions, guided only by a textual “meta-prompt” that includes solution history and performance metrics.
Why OPRO Matters
-
Eliminates the need for formal solvers: You don’t need specialized optimization code; you simply need an objective function and a way to track solution trajectories.
-
Offers unparalleled flexibility: LLMs excel at interpreting natural language constraints, examples, and instructions. This dramatically simplifies the specification of complex or creative constraints (e.g., “the solution must be concise and engaging”).
-
Delivers competitive performance: While OPRO won’t always outperform specialized solvers on large-scale problems, it achieves remarkable results on moderately sized tasks—particularly those without established optimization methods, such as prompt optimization itself.
-
Democratizes optimization: The approach makes sophisticated optimization techniques accessible to users without deep mathematical or programming expertise.
2. The OPRO Framework: How It Works
OPRO operates through an elegantly simple yet powerful feedback loop:
Core Components
-
Objective Function Evaluator
This black-box function computes the score or loss for each candidate solution. For example, when optimizing a prompt for math problems, the score might be the accuracy achieved by that prompt on a validation set. -
Meta-Prompt
The meta-prompt serves as the textual “driver” that guides the LLM’s optimization process. It typically contains:- A clear description of the task and expected solution format
- A history of previously generated solutions and their evaluation scores
- Explicit instructions to generate new solutions that outperform previous attempts
- Optional: constraints, examples, or domain-specific guidance
-
LLM as the Optimizer
The language model functions as the optimization engine. At each iteration:- The LLM receives the meta-prompt (including solution history and scores)
- It proposes one or more new candidate solutions
- Each new solution is evaluated using the objective function
- The best new solutions (with their scores) are incorporated into the meta-prompt for the next iteration
-
Stopping Criteria
The optimization process continues until reaching a predefined maximum number of iterations or until the LLM cannot improve upon the best solutions found so far.
The Optimization Loop

Key Innovation
What makes OPRO particularly powerful is how the LLM implicitly manages the “exploration vs. exploitation” trade-off based on natural language instructions in the meta-prompt. By adjusting phrases like “Find solutions that are substantially different from previous ones” versus “Make small improvements to the best solution,” users can guide the optimization strategy without formal mathematical expressions.
The sampling temperature also plays a crucial role: moderate temperatures (around 1.0) help balance between leveraging past successes and exploring new approaches.
3. Case Studies: OPRO in Action
Let’s examine how OPRO performs across different optimization domains, from simple numerical problems to complex combinatorial challenges.
3.1 Linear Regression: A Foundational Example
Linear regression offers an intuitive starting point for understanding OPRO. Consider the task of finding parameters  that minimize the sum of squared errors (SSE) for a dataset:
that minimize the sum of squared errors (SSE) for a dataset:

Here’s how OPRO tackles this problem:
import random
def sse(w, b, X, Y):
"""Compute Sum of Squared Errors for a dataset."""
return sum((y - (w*x + b))**2 for x, y in zip(X, Y))
# Generate synthetic data
X = list(range(1, 51))
w_true, b_true = 3, 10
Y = [w_true*x + b_true + random.gauss(0, 1) for x in X]
# Initialize with random solutions
solutions = [(random.uniform(0, 5), random.uniform(0, 15), 0) for _ in range(5)]
for i in range(len(solutions)):
w, b, _ = solutions[i]
error = sse(w, b, X, Y)
solutions[i] = (w, b, error)
def build_meta_prompt(solutions):
# Sort solutions by their SSE (ascending = better)
solutions_sorted = sorted(solutions, key=lambda s: s[2])
text = "# Linear Regression Optimization\n\n"
text += "Find values for w and b that minimize the Sum of Squared Errors (SSE).\n\n"
text += "## Previous Solutions (ordered from worst to best):\n\n"
for w_, b_, val in solutions_sorted:
text += f"* w={w_:.4f}, b={b_:.4f} → SSE={val:.2f}\n"
text += "\n## Your Task:\n"
text += "Propose NEW values for (w, b) that will yield an EVEN LOWER SSE than the best solution above.\n"
text += "Consider patterns in how the SSE changes with different parameter values.\n"
text += "Format each solution as: (w=X.XXX, b=Y.YYY)\n"
return text
# Function to query the LLM for new solution candidates
def ask_llm_for_solutions(prompt, n=4, temperature=1.0):
"""
Query the LLM to generate new candidate solutions.
Args:
prompt: The meta-prompt containing problem description and solution history
n: Number of solutions to generate
temperature: Sampling temperature (higher = more exploration)
Returns:
List of (w, b) tuples representing new candidate solutions
"""
# In practice, this would call an actual LLM API
# This is a placeholder for demonstration
# Example return: [(2.9845, 9.9762), (3.0124, 10.0215), ...]
pass
num_steps = 10
for step in range(num_steps):
# Build the meta-prompt
prompt = build_meta_prompt(solutions)
# Query the LLM for new guesses (typically 3-5)
new_candidates = ask_llm_for_solutions(prompt, n=4, temperature=1.0)
# Evaluate each new candidate
for (w_guess, b_guess) in new_candidates:
val = sse(w_guess, b_guess, X, Y)
solutions.append((w_guess, b_guess, val))
# Optional: Keep only top N solutions to manage context length
solutions = sorted(solutions, key=lambda s: s[2])[:15]
# Report the best solution
best = min(solutions, key=lambda s: s[2])
print(f"Best solution found: w={best[0]:.4f}, b={best[1]:.4f}, SSE={best[2]:.2f}")
print(f"True values were: w={w_true}, b={b_true}")Remarkably, even on this simple problem, LLMs can identify patterns in the solution space and converge toward better parameters over time. The model discerns which direction in the parameter space leads to error reduction by examining the trajectory of previous solutions.
3.2 Traveling Salesman Problem (TSP)
The Traveling Salesman Problem represents a classic NP-hard combinatorial optimization challenge: find the shortest route that visits every city exactly once and returns to the starting point.
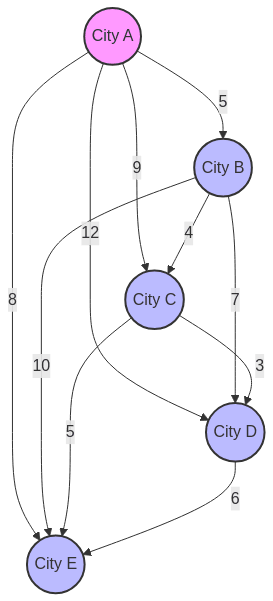
For TSP, the OPRO approach works as follows:
- Objective: Calculate the total distance of a proposed route.
- Meta-prompt: Include city coordinates, previously tried routes, and their total distances.
- Solution Generation: The LLM proposes new permutations of cities.
A sample meta-prompt might look like:
# Traveling Salesman Problem Optimization
## Cities:
A: (0, 0)
B: (1, 3)
C: (4, 2)
D: (3, 5)
E: (7, 1)
## Previous Routes:
Route: A → B → C → D → E → A, Distance: 24.1
Route: A → C → B → D → E → A, Distance: 22.7
Route: A → E → D → C → B → A, Distance: 20.3
## Your Task:
Propose a NEW route that has a SHORTER total distance than the best route above.
Consider which segments contribute most to the total distance.While OPRO might not match specialized TSP solvers on large instances (50+ cities), it performs surprisingly well on small to medium instances (10-20 cities), often discovering optimal or near-optimal solutions within a few iterations.
4. Prompt Optimization: OPRO’s Killer Application
Perhaps the most compelling use case for OPRO is Prompt Optimization—finding better prompts for an LLM on a particular task. This application highlights OPRO’s strengths in navigating purely textual solution spaces where traditional optimization methods struggle.
The Self-Improvement Loop
The process works like this:
-
Task Definition: Select a downstream task (e.g., solving grade-school math problems) with a dataset of question-answer pairs.
-
Objective Function: For each candidate prompt (instruction), compute its effectiveness—typically measured as accuracy on a small training set.
-
OPRO Loop:
- Track the best prompts and their performance metrics
- Include example QA pairs in the meta-prompt
- Ask the LLM to generate new prompts that might outperform the current best

Practical Implementation
Here’s a simplified code example for prompt optimization:
def compute_instruction_accuracy(instruction, training_data, model):
"""Calculate the accuracy of a given instruction prompt."""
correct = 0
for question, correct_answer in training_data:
# Combine instruction with question
prompt = f"{instruction}\n\nQuestion: {question}\nAnswer:"
# Query the LLM
model_answer = model.generate(prompt)
# Evaluate correctness
if is_answer_correct(model_answer, correct_answer):
correct += 1
return 100.0 * correct / len(training_data)
# Start with baseline instructions
instructions = [
"Solve the following problem.",
"Think step by step.",
"Let's be careful and solve this math problem."
]
# Evaluate initial instructions
solutions = [(instr, compute_instruction_accuracy(instr, training_data, model))
for instr in instructions]
def build_meta_prompt(solutions, example_problems):
# Sort by performance (ascending order)
sorted_sols = sorted(solutions, key=lambda s: s[1])
prompt = "# Prompt Optimization for Math Problem Solving\n\n"
prompt += "## Previous Instructions and Their Accuracy:\n\n"
for instr, acc in sorted_sols:
prompt += f"Instructions: \"{instr}\"\nAccuracy: {acc:.1f}%\n\n"
prompt += "## Example Problems from the Dataset:\n\n"
for question, answer in example_problems:
prompt += f"Question: {question}\nCorrect Answer: {answer}\n\n"
prompt += "## Your Task:\n"
prompt += "Generate a NEW instruction that will help the model solve these math problems more accurately.\n"
prompt += "Your instruction should be different from the previous ones and likely achieve higher accuracy.\n"
prompt += "Be creative but focused on improving mathematical reasoning and step-by-step thinking.\n"
return prompt
def generate_with_llm(prompt, n=5, temperature=1.0):
"""
Generate new candidate instructions using an LLM.
Args:
prompt: The meta-prompt containing prior instructions and their performance
n: Number of instructions to generate
temperature: Sampling temperature (higher = more creative)
Returns:
List of strings containing new instruction prompts
"""
# In practice, this would call an actual LLM API
# This is a placeholder for demonstration
# Example return: ["Solve this math problem step-by-step...", "Break down the problem..."]
pass
for iteration in range(20):
# Select a few example problems to show in the meta-prompt
examples = random.sample(training_data, 3)
# Build the meta-prompt
prompt = build_meta_prompt(solutions, examples)
# Generate new candidate instructions
new_instructions = generate_with_llm(prompt, n=5, temperature=1.0)
# Evaluate new instructions
for instr in new_instructions:
accuracy = compute_instruction_accuracy(instr, training_data, model)
solutions.append((instr, accuracy))
# Keep only top performers to manage context length
solutions = sorted(solutions, key=lambda s: s[1], reverse=True)[:10]
# Report progress
best_instr, best_acc = solutions[0]
print(f"Iteration {iteration}, Best accuracy: {best_acc:.1f}%, Instruction: \"{best_instr}\"")Empirical Results
The OPRO approach to prompt optimization has achieved remarkable results:
- GSM8K (grade-school math): Improvements of +8-12% over standard human-crafted prompts
- Big-Bench Hard: Gains up to +50% on certain reasoning tasks
- Coding tasks: Significant improvements in code generation quality and correctness
For example, a standard prompt like “Let’s think step by step” might yield 61% accuracy on a math dataset, while an OPRO-discovered prompt such as “I’ll solve this step-by-step, tracking units carefully and double-checking my arithmetic at each stage” might achieve 73% accuracy.
5. Practical Considerations and Best Practices
To achieve optimal results with OPRO, consider these practical guidelines:
5.1 Meta-Prompt Engineering
The meta-prompt design significantly impacts OPRO’s effectiveness:
- Clear task definition: Precisely describe what constitutes a good solution
- Solution history organization: Sort from worst to best to leverage the recency bias of LLMs
- Explicit improvement instructions: Clearly ask for “solutions that outperform the best current solution”
- Constraint reminders: Reiterate key constraints that solutions must satisfy
5.2 Balancing Exploration and Exploitation
Finding the right balance between exploring new solution regions and refining existing good solutions is critical:

- Temperature control: Use temperature ~1.0 for most applications; adjust higher (more exploration) or lower (more exploitation) based on problem needs
- Diversity instructions: Include explicit requests for solution diversity when appropriate
- Multiple candidates per iteration: Generate 4-8 solutions per step to increase the chances of improvement
5.3 Managing Solution History
As the optimization progresses, the solution history grows, potentially exceeding the LLM’s context window:
- Selective retention: Keep only the top-performing solutions plus a few diverse lower-performing ones
- Trajectory sampling: Include solutions from different stages of the optimization process to maintain diversity
- Summarization: For longer runs, summarize patterns observed in previous solutions
5.4 Avoiding Common Pitfalls
Several challenges may arise when implementing OPRO:
- Overfitting: Solutions may excel on the training set but generalize poorly; maintain a separate validation set
- LLM limitations: Models might hallucinate impossible solutions; verify feasibility
- Repetitive solutions: The LLM might propose very similar candidates; explicitly request diversity
- Performance plateaus: Progress often stalls after initial improvements; try reframing the problem or increasing temperature
6. Limitations and Future Directions
While OPRO offers many advantages, understanding its limitations is essential:
OPRO vs. Traditional Optimization Methods
| Aspect | OPRO | Traditional Methods |
|---|---|---|
| Problem Specification | Natural language | Mathematical formulation |
| Implementation Effort | Low (prompting only) | Medium to high (algorithm-specific) |
| Domain Knowledge Required | Minimal | Often extensive |
| Constraint Handling | Flexible, natural language | Formal, explicit constraints |
| Performance on Small Problems | Excellent | Very good to excellent |
| Performance on Large Problems | Limited by context window | Often scales better |
| Computational Cost | Higher (multiple LLM calls) | Generally lower |
| Explainability | High (rationale in natural language) | Variable (algorithm-dependent) |
Current Limitations
- Scaling challenges: Performance degrades on large-scale problems (e.g., TSP with 50+ cities)
- Context window restrictions: Limited by how much solution history can fit in the prompt
- Dependence on LLM capabilities: The optimizer is only as good as the underlying language model
- Computational efficiency: Multiple LLM calls make OPRO more expensive than some traditional methods
Future Research Directions
Several promising research avenues could address these limitations:
- Hierarchical optimization: Using multiple OPRO loops at different abstraction levels
- Hybrid approaches: Combining OPRO with traditional optimization methods
- Adaptive meta-prompting: Automatically adjusting the meta-prompt based on optimization progress
- Cross-model optimization: Using one LLM to optimize prompts for another, potentially smaller model

7. Conclusion: The OPRO Revolution
OPRO represents a paradigm shift in how we approach optimization problems. By recasting optimization as a dialogue with a language model about improving solutions, we unlock new capabilities that were previously inaccessible or required specialized expertise.
This framework’s most significant contribution is demonstrating that LLMs can function as general-purpose optimizers, extracting patterns from solution histories to propose systematically better candidates. OPRO is particularly transformative for prompt optimization, where the “search space” is purely textual and domain knowledge is challenging to formalize.
As language models continue to advance in reasoning capabilities, we can expect OPRO to become even more powerful, potentially revolutionizing how we approach a wide range of optimization challenges in scientific research, engineering, and AI development.
Resources
- OPRO GitHub (official implementation):
https://github.com/google-deepmind/opro - Original Paper:
“Large Language Models as Optimizers,” Yang et al. (2023)
Bottom Line: OPRO demonstrates that with cleverly designed prompts and feedback loops, a single LLM can evolve from being merely a prediction engine to becoming a sophisticated optimization system—all without any additional training or fine-tuning. This Optimization by PROmpting approach opens new possibilities for solving complex problems through the power of natural language.