Executive Summary
Large language models like GPT-4 and Claude have this uncanny ability to learn from examples you feed them in the prompt, right there in the context window, without needing any weight updates. You show them a pattern, they pick it up. This “in-context learning” has been a bit of a puzzle: how do these massive networks adapt so fluidly on the fly?
Recent, rather profound research from Google DeepMind offers a powerful answer: Transformers are more than just pattern matchers; they develop internal optimization algorithms—these so-called “mesa-optimizers”—that effectively run something akin to gradient descent during the forward pass. Yeah, you read that right. While processing your prompt, the model is running its own optimization routine, tuning itself to your specific examples in real-time.
Let’s unpack this rather profound discovery, digging into how Transformers seem to spontaneously evolve these internal learning capabilities and how the researchers even cooked up specialized “mesa-layers” to make this whole process more explicit and, potentially, more potent.
Introduction: The Mystery of In-Context Learning
You feed a hefty language model a few examples like this:
Input: 5 → Output: 25
Input: 10 → Output: 100
Input: 7 → ?And bam, it spits out “49”. No fine-tuning, no parameter tweaks. Just pure adaptation from the prompt. This knack for grabbing onto new patterns solely from context examples is what we call “in-context learning.” But how the hell do Transformers pull off this magic trick?
For a while, the go-to explanation involved “induction heads”—specialized attention mechanisms, clever pattern-matching tricks that could copy sequences seen earlier in the context. Useful, sure, but it felt a bit thin, especially for explaining the sophisticated adaptation seen in the bigger, beefier models.
Now, the DeepMind crew has unearthed a deeper, more potent mechanism: mesa-optimization. Their work suggests that during the grind of standard pre-training, Transformers don’t just learn to predict the next word; they actually bootstrap internal optimization algorithms. These algorithms perform operations remarkably similar to gradient descent, all humming along quietly during the forward pass.
It fundamentally reframes how we think about these models’ capabilities and points towards potentially radical architectural shifts down the road.

1. From “Induction Heads” to “Mesa-Optimizers”
The Induction Head Explanation
Early spelunking into Transformer guts revealed these “induction heads.” They’re essentially attention patterns wired to perform lookups. Given something like:
“Alice lives in Paris. Bob lives in London. Alice speaks ___”
An induction head could trace the pattern: find “Alice”, look ahead to “lives”, then “in”, then grab “Paris”, helping the model predict “French”. Clever pattern matching, but it doesn’t quite capture the feeling of genuine learning we observe.
Entering the Mesa-Optimizer
The DeepMind paper goes way beyond simple pattern retrieval. It demonstrates that well-trained Transformers aren’t just recalling facts; they’re actively optimizing an internal representation on the fly:
- Token Binding Phase: Early layers act like data collectors, gluing consecutive tokens together, aggregating context into meaningful chunks.
- Gradient-Based Update Phase: Deeper layers then take these chunks and start massaging them, performing operations that mathematically mirror gradient descent steps on some internal objective.
This two-step dance—gather relevant context, then optimize—is how Transformers manage to adapt instantly. They essentially implement “learning to learn” right there within their forward pass, no external training loop required.
2. What Is “Mesa-Optimization”?
Understanding the Terminology
Let’s break down the jargon. “Mesa” – Spanish for table, think flat-topped mountain. In AI, it signals a nested optimization setup:
- Base Optimization: The familiar outer loop. This is standard model training, where backpropagation tweaks the Transformer’s weights based on predicting the next token across vast datasets.
- Mesa-Optimization: An internal optimization process that spontaneously emerges within the trained Transformer. This algorithm executes during the forward pass whenever the model encounters new input.
Think of it like this: While you’re busy training the main model (base optimization), it quietly develops its own little optimization algorithm (mesa-optimization) that it runs automatically to handle new data it sees at inference time.

Why Mesa-Optimizers Emerge Naturally
Why would this even happen? When you train a Transformer on incredibly diverse data, full of countless different patterns, tasks, and structures, it faces a gnarly problem: how to generalize without just memorizing everything?
The solution it seems to stumble upon is remarkably elegant: learn a general-purpose optimization routine. Instead of learning specific answers, learn how to find the answers based on the immediate context. Mathematically, the Transformer learns to approximate something like this internal update:
Where is some internal parameter vector, distinct from the model’s main weights, that gets tweaked during the forward pass.
This isn’t magic; it’s an emergent property. It’s valuable because it lets the model:
- Adapt rapidly to new tasks without needing fine-tuning.
- Tackle problems structurally similar but superficially different from its training data.
- Perform reasoning that feels more sophisticated than just copying patterns.
3. The Mechanics: How a Single Attention Layer Can Implement Gradient Descent
Here’s one of the paper’s more elegant twists: a single self-attention layer, the core building block of a Transformer, can be configured to perform exactly one step of gradient descent.
Consider a simple regression task where the model sees a sequence of pairs. The researchers showed that with the right weight matrices (which can be learned during standard training), the attention mechanism can compute an update such that:
Basically, the output of the layer represents an updated internal parameter state, refined by one gradient step based on the current input pair.
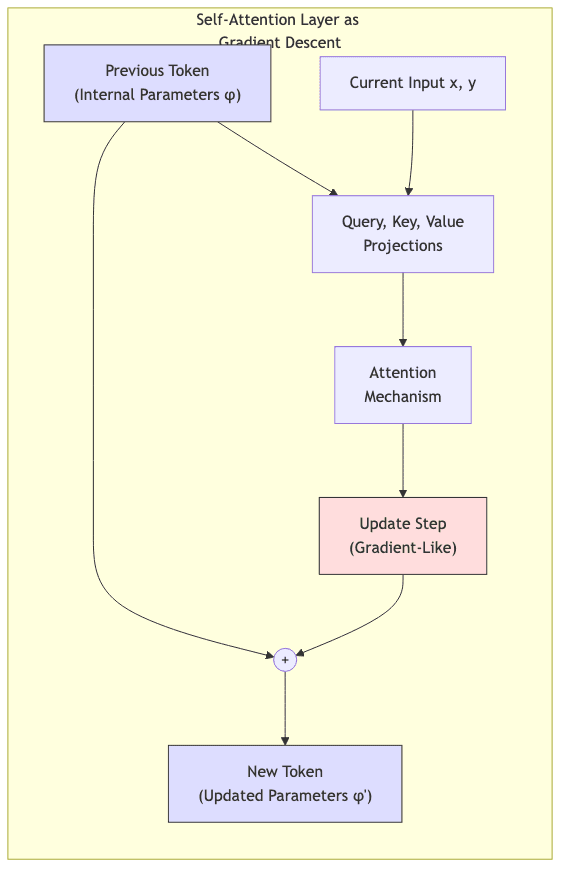
Here’s a conceptual sketch in Python showing the idea:
import torch
def single_step_gradient_descent(previous_token, current_x, current_y, learning_rate):
"""
Conceptual demonstration: How linear self-attention could mimic
one step of gradient descent on a squared-error objective.
NOTE: This is illustrative; the actual learned weights are complex.
Parameters:
- previous_token: Encodes the current state of our internal model parameter Φ
(potentially includes history)
- current_x: Current input
- current_y: Current target output
- learning_rate: Step size for gradient update (implicitly learned)
Returns:
- new_token: Updated representation encoding refined Φ'
"""
# These weight matrices (Wk, Wq, Wv, P) are LEARNED during pre-training
# such that the overall operation approximates a gradient step.
# (1) Project the previous token state to create the "key"
key = Wk @ previous_token
# (2) Project current input/output to create the "query"
query = Wq @ torch.cat([current_x, current_y], dim=0)
# (3) The "value" is constructed to encode necessary gradient information
# (Implementation details highly simplified here)
value = Wv @ previous_token
# (4) Attention computes an update mathematically equivalent to a gradient step
# The attention score weights the gradient information in 'value'
attention_score = key @ query # Simplified attention calculation
weighted_value = value * attention_score # Apply attention weight
delta = P @ weighted_value # Project to get the update delta
# (5) The residual connection performs the update: Φ' = Φ + ΔΦ
new_token = previous_token + delta
return new_tokenYou wouldn’t design these Wk, Wq, Wv, P matrices by hand, obviously. The kick is that standard next-token prediction training can spontaneously discover weights that make the attention mechanism compute something equivalent to partial derivatives and the residual connection perform the update step. It’s an elegant repurposing of existing machinery.
This explains how even shallow Transformers can exhibit basic in-context learning.
4. Going Deeper: Multi-Layer Transformers as Multi-Step Optimizers
In the deeper Transformers we use today, stacking multiple attention layers allows this mesa-optimization process to become more sophisticated, layered, almost iterative:
-
Early Layers (say, 1-2): Focus on grabbing context, binding related tokens, essentially setting up the problem representation.
-
Middle Layers (say, 3-6): Start performing the core gradient-like updates, beginning to refine the internal parameters
based on the examples seen so far.
-
Later Layers (say, 7+): Continue the optimization dance, potentially implementing more complex updates – maybe incorporating momentum-like effects or adaptive learning rate analogues.
By the time an input token has traversed the entire stack, the model has effectively run multiple steps of its internal optimization algorithm. It converges towards a set of internal parameters suited for the specific task defined by the examples in the prompt.
This multi-step view neatly explains why giving LLMs more examples in the prompt often dramatically improves performance. Each example provides another data point for the internal mesa-optimizer to chew on, refining its internal parameters further – just like feeding more batches to a standard gradient descent process improves a traditional model.
5. The “Mesa-Layer”: Making Internal Optimization Explicit
Building on these insights, the DeepMind team cooked up a novel architectural twist: the mesa-layer. It’s a specialized variant of self-attention that doesn’t just implicitly approximate optimization, it explicitly solves a regularized least-squares problem at each step.

The core idea is that for each token position , the layer calculates an optimal parameter matrix
for each attention head
by minimizing a ridge regression objective over the keys
and values
seen so far:
And then applies this to the current query
to produce the output:
In essence, each attention head solves a mini regression problem in closed form. The researchers showed how to implement this efficiently using recursive updates (leveraging the Sherman-Morrison formula for matrix inversion updates), avoiding a full matrix solve at every step.
Here’s a high-level sketch of that logic:
def mesa_layer(keys, values, queries, lambda_reg=0.1):
"""
Conceptual sketch of a 'mesa' layer explicitly solving regularized
least-squares at each time step. Efficient implementation uses
recursive updates (Sherman-Morrison).
Parameters:
- keys: Sequence of key vectors [k_1, ..., k_t]
- values: Sequence of value vectors [v_1, ..., v_t]
- queries: Sequence of query vectors [q_1, ..., q_t]
- lambda_reg: Regularization strength
Returns:
- outputs: Sequence of output vectors
"""
# Dimensions
d_key = keys[0].shape[0]
d_value = values[0].shape[0]
# Initialize recursive components for (K^T K + lambda*I)^(-1) and K^T V
# R_inv corresponds to (K^T K + lambda*I)^(-1)
R_inv = (1.0/lambda_reg) * torch.eye(d_key)
# v_k_sum corresponds to V^T K (or similar, depending on exact formulation)
v_k_sum = torch.zeros((d_value, d_key))
outputs = []
for t in range(len(queries)):
k_t = keys[t] # shape [d_key]
v_t = values[t] # shape [d_value]
q_t = queries[t] # shape [d_key]
# Update the sum V^T K part (conceptually)
# Note: Actual efficient implementation updates v_k_sum differently
v_k_sum += torch.outer(v_t, k_t) # outer product is [d_value, d_key]
# Efficiently update R_inv using Sherman-Morrison formula
# R_inv_new = R_inv_old - (R_inv @ k_t @ k_t.T @ R_inv) / (1 + k_t.T @ R_inv @ k_t)
numerator = R_inv @ torch.outer(k_t, k_t) @ R_inv
denominator = 1.0 + k_t @ R_inv @ k_t
R_inv = R_inv - numerator / denominator
# Compute Phi_hat = v_k_sum @ R_inv (conceptually)
# Then apply to query: output = Phi_hat @ q_t
# The actual computation combines these steps
output_t = v_k_sum @ R_inv @ q_t # shape [d_value]
# Potentially apply a final output projection P_h (omitted for simplicity)
# output_t = projection_matrix @ output_t
outputs.append(output_t)
return outputsEmpirically, this mesa-layer consistently did better than standard attention on tasks that clearly involved underlying linear dynamics or system identification. Making the optimization explicit seems to yield better sample efficiency for in-context learning.
6. Experimental Evidence: Mesa-Optimization in Action
The researchers put these ideas to the test on sequences generated by various underlying processes.
Linear and Nonlinear System Identification
They fed Transformers sequences from:
- Fully Observed Linear Systems: Simple
dynamics.
- Partially Observed Linear Systems: Where only some dimensions of
are visible.
- Nonlinear Systems: Using MLPs,
.
Across the board, standard Transformers learned internal algorithms that looked like mesa-optimization: binding tokens early, then performing updates later. For the partially observed case, it was neat to see the models implicitly learn to maintain an internal state representation, effectively rediscovering concepts akin to Kalman filters. The explicit mesa-layer architecture generally outperformed standard attention here.
Emergent Few-Shot Learning Capabilities
Perhaps the slickest demonstration: Transformers trained only on next-token prediction were then tested on few-shot regression tasks presented purely in-context. Given a sequence of pairs defining a new problem, the models’ internal mesa-optimizers kicked in automatically.
Prediction accuracy improved as more examples were provided, tracing learning curves that looked remarkably like explicit gradient descent. This provides a compelling mechanism for how LLMs achieve few-shot learning without any explicit meta-training.
The “Early Ascent” Phenomenon
One curious observation was the “early ascent”: sometimes, prediction error would briefly increase after the first couple of examples before rapidly improving. This mirrors the behavior of standard optimization algorithms when initial data points suggest spurious patterns. They found that techniques like adding an End-of-Sequence token or using learned prompt prefixes helped mitigate this – a nod to the dark arts of prompt engineering that practitioners wrestle with daily.
7. Broader Implications for AI Research and Development
Unifying Multiple Explanations of In-Context Learning
The mesa-optimization lens neatly snaps several previous theories about in-context learning into focus:
| Theory | Relation to Mesa-Optimization |
|---|---|
| Induction Heads | A simpler, specialized form focused on pattern copying |
| Kernel Regression | The attention mechanism acts like a kernel method because it’s implicitly solving regression-like problems |
| Meta-Learning | The Transformer learns to learn organically, without needing an explicit meta-objective during training |
Architectural Improvements Inspired by Mesa-Optimization
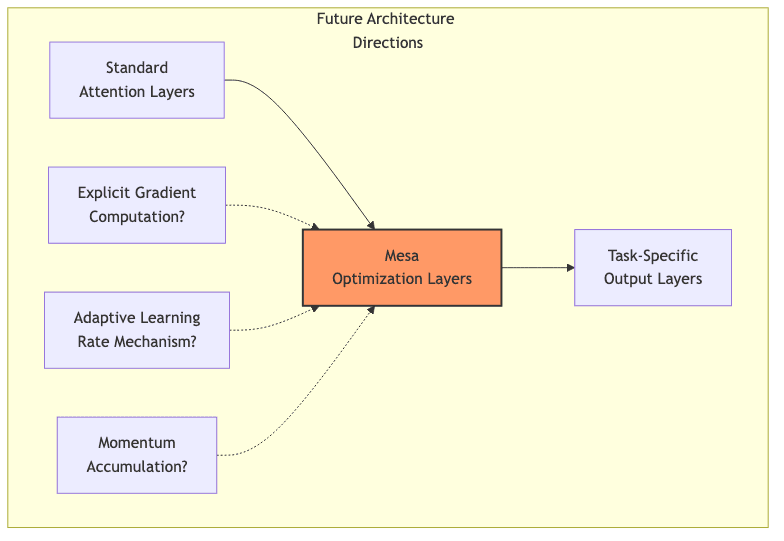
This understanding opens up interesting avenues for future model design:
- Explicit Optimization Layers: Go beyond the initial mesa-layer. Design layers purpose-built for gradient-like updates.
- Hybrid Architectures: Maybe future models will be “hybrid beasts,” mixing standard attention with specialized optimization modules.
- Interpretability Tools: This framework offers new lenses for peering inside the black box and understanding how models adapt.
The Naturalness of Advanced Capabilities
Perhaps the most profound takeaway is how complex capabilities like in-context learning seem to emerge organically from a simple objective (next-token prediction) when you have enough scale (parameters + data diversity). It suggests the ability to adapt and learn isn’t necessarily something you have to explicitly build in; it can be an emergent property of training sufficiently powerful generalist models.
This resonates with the surprising emergent abilities we’ve seen as language models have scaled, hinting that more such “free lunches” might be waiting as scale increases further.
8. Conclusion: What Mesa-Optimization Tells Us About the Future of AI
The discovery of mesa-optimization inside Transformers is more than just a clever finding; it’s a potential paradigm shift in understanding LLMs. These models aren’t static lookup tables; they are dynamic systems that run their own internal optimization routines on the fly.
Key implications tumble out from this:
- In-context learning is potent: It’s not just pattern matching; it’s closer to genuine, albeit limited, optimization, enabling adaptation to a broader task range.
- Architecture matters: Explicitly baking optimization mechanics into layers (like the mesa-layer) can boost performance and efficiency.
- Training vs. Inference blur: Models that optimize during inference muddy the traditional clean separation between training and deployment.
- Expect emergent weirdness: If mesa-optimization arises spontaneously, what other complex cognitive algorithms might be bootstrapping themselves inside these networks as they scale?
For those building with LLMs, this offers deeper intuition for why prompting strategies work (or don’t). For researchers, it carves out new paths for architecture design, potentially leading to models that learn faster and generalize better by leaning into these internal optimization dynamics more deliberately.
We might be seeing the early outlines of AI systems that don’t just process information, but actively learn and adapt within the span of a single interaction. The ghost isn’t just in the machine; it’s running gradient descent.
Further Resources
-
Original Paper: Uncovering Mesa-Optimization Algorithms in Transformers, von Oswald et al. (Google DeepMind), Sept 2023. [arXiv:2309.05858]
-
Related Works:
- Transformers Learn In-Context by Gradient Descent by von Oswald et al. (2023)
- In-context Learning and Induction Heads by Olsson et al. (Anthropic Blog Post/Paper likely refers to work like arXiv:2209.11895)
- What Learning Algorithm is In-Context Learning? Investigations with Linear Models by Akyürek et al. (2022) [arXiv:2211.15661]
-
Implementation Resources:
- GitHub: Mesa-Optimization Demo Code (Note: Actual DeepMind repo might contain illustrative code, check availability)
- Colab Notebook: Exploring Mesa-Layers (Note: A community or official notebook might exist or could be created based on the paper/repo)
Note to Readers: This stuff is on the cutting edge. We’ve glossed over some gnarly math for clarity, aiming for the core concepts. If you want the full technical deep dive, the original paper awaits.