Introduction
For any practitioner operating outside the blessed sanctuaries of massive data centers, Parameter-Efficient Fine-Tuning (PEFT) is no less than a lifeline. Among the PEFT catechisms, Low-Rank Adaptation (LoRA) became the default rite. By injecting a pair of small, trainable matrices into a model’s existing weights and freezing the gargantuan originals, LoRA offered a tantalizingly close approximation of full fine-tuning at a fraction of the computational cost. We all adopted it.
But living with LoRA meant living with its quirks. My own experience, echoed across the community, revealed a few persistent, nagging issues:
- Its performance can be maddeningly sensitive to the choice of rank r and other hyperparameters.
- A small but undeniable performance gap often remains between LoRA and a full, scorched-earth fine-tune.
- A deeper, more fundamental question lingered: Why should every low-rank update be shackled to a magnitude proportional to the original pre-trained weights?
Enter Weight-Decomposed Low-Rank Adaptation (DoRA). This technique, introduced by Liu et al. earlier this year, offers a principled answer. It deconstructs each pre-trained weight matrix into two distinct components: a direction and an independent magnitude. By making both the direction (via LoRA) and the magnitude trainable, it decouples the update’s scale from its content.
In this post, I’ll walk through the mechanics of DoRA, share a practical implementation for fine-tuning Mistral-7B using the Hugging Face PEFT library, and dissect the empirical results from my own consumer-grade hardware.
From LoRA to DoRA: The Core Idea
To grasp DoRA, we first have to deconstruct LoRA. For a pre-trained weight matrix , LoRA approximates its update
with a low-rank decomposition
, where
,
, and the rank
is kept small (
). The final weight matrix
is:
(The scaling factor can vary; PEFT uses
lora_alpha for and often initializes it to
r).
DoRA’s insight is to challenge the monolithic nature of . It starts by factorizing the pre-trained weight matrix itself into a magnitude vector
and a direction matrix
:
Here, holds the directional information, and the vector
captures the magnitude for each corresponding row or column. The crucial step is what happens next: DoRA applies the LoRA update only to the directional component
, while simultaneously making the magnitude vector
trainable.
The fine-tuned weight matrix is then reconstructed as:
Where is the standard LoRA update, but for the direction matrix, and
is the learned adjustment to the magnitude. This clean separation allows the optimizer to adjust the scale of the updates independently of their direction, freeing them from the constraints imposed by the initial magnitudes in
.
The additional parameter count from the trainable magnitude vector is almost negligible-often less than 0.01% for a large model-yet this architectural tweak can yield significant improvements in performance and stability.
Here is a conceptual diagram of how DoRA breaks down and rebuilds a pre-trained weight:
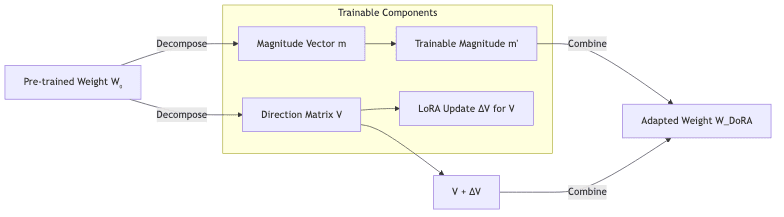
(The conceptual flow of DoRA: Decompose, Adapt, Recombine)
A Minimal DoRA Recipe for Mistral-7B with PEFT
Fortunately, migrating an existing LoRA setup to DoRA is almost trivial. Hugging Face’s PEFT library (v0.10+) has integrated DoRA support directly into its LoraConfig, requiring little more than flipping a boolean flag.
Here is the configuration I used to fine-tune Mistral-7B:
from peft import LoraConfig, TaskType
peft_config = LoraConfig(
r=16,
lora_alpha=16, # Typically set to r or 2*r
lora_dropout=0.05,
bias="none",
use_dora=True, # The magic flag that enables DoRA
task_type=TaskType.CAUSAL_LM,
target_modules=[
"q_proj", "k_proj", "v_proj", "o_proj", # Attention projections
"gate_proj", "down_proj", "up_proj" # MLP linear layers
]
)Hardware and Optimization Checklist
Getting this to run on a consumer rig-in my case, a 24GB RTX 4090-demands a familiar set of optimizations. Success hinges on a setup like this:
| Item | My Setup / Recommendation |
|---|---|
| GPU | 24 GB VRAM (e.g., NVIDIA RTX 3090/4090) |
PyTorch dtype | bfloat16 (Ampere architecture or newer) or float16 |
| Flash Attention | Enabled (requires compatible GPU & PyTorch) |
| Gradient Checkpointing | Enabled to claw back memory |
| Sequence Length | ≤ 1024 (adjust based on VRAM pressure) |
Using bfloat16 and Flash Attention 2 is non-negotiable for maximizing throughput and minimizing the memory footprint.
Dataset and Training Loop
For this experiment, I fine-tuned Mistral-7B on a subset of the Open-Orca/OpenOrca dataset, a workhorse for instruction tuning. The training ran for three epochs with a per-device batch size of 3 and gradient accumulation steps of 6, creating an effective batch size of 18-a classic memory-for-compute trade.
Tips for Squeezing DoRA into Smaller GPUs (e.g., 12-16GB VRAM)
For those operating on the bleeding edge of VRAM capacity, DoRA remains viable with aggressive optimization:
- Slash Sequence Length: Halving the sequence length to 512 or even 256 is the most effective way to cut memory usage.
- Trade Batch Size for Accumulation: Maintain a reasonable global batch size by increasing gradient accumulation steps while dropping the per-device batch size to 1 if you must.
- Lower the Rank
r: DoRA is often more potent at lower ranks than LoRA. Anrof 8 or even 4 is a reasonable starting point. - Target Fewer Modules: If memory is still too tight, restrict DoRA to just the MLP linear layers (
gate_proj,down_proj,up_proj) or even just the core attention query and value projections. - Embrace Quantization (QDoRA): PEFT’s DoRA implementation integrates with
bitsandbytesfor 4-bit or 8-bit quantized base models. This is QDoRA. It massively reduces the base model’s memory footprint, making fine-tuning far more accessible on smaller hardware.
My Experimental Results
I evaluated both LoRA and DoRA fine-tuned versions of Mistral-7B. Here’s a summary of what I observed.
Training Loss
In my runs, the LoRA model showed a slightly faster drop in training loss initially. However, the DoRA model ground its way to a lower final training loss by the end of the third epoch. The validation loss for both models remained relatively flat, a common phenomenon when instruction-tuning on smaller datasets where the model can quickly memorize the training distribution.
Zero-Shot Accuracy (via Evaluation Harness)
I used the EleutherAI LM Evaluation Harness to benchmark zero-shot performance on HellaSwag and ARC-Challenge. The normalized accuracy (acc_norm) provides a more robust comparison:
| Task | DoRA (r=16) | LoRA (r=16) |
|---|---|---|
| HellaSwag (acc_norm) | 0.82 | 0.819 |
| ARC-Challenge (acc_norm) | 0.559 | 0.561 |
The results are close, well within the margin of error for a single training run. LoRA eked out a win on ARC-Challenge, while DoRA was marginally better on HellaSwag. These small differences confirm that DoRA is a viable and competitive alternative, not a silver bullet, but a tool with a different set of trade-offs.
Training Speed and Inference Latency
It is critical to understand the practical costs of DoRA. Elegance is rarely free.
- Instantiation Overhead: I observed that calling
get_peft_modelwithuse_dora=Trueis noticeably slower than with standard LoRA. This is a known papercut, and the PEFT library is actively working on improvements. - Training Throughput: The price of decomposition is paid during training. In my setup, a training step with DoRA was roughly 1.5x to 1.8x slower than an identical LoRA run. This is due to the extra computations needed to handle the decomposed weights and trainable magnitudes.
- Inference: To avoid carrying this overhead into production, it is non-negotiable to merge the adapter weights back into the base model with
model.merge_and_unload(). This collapses the adapter and restores inference speed to that of the original model. Merging adapters from quantized base models (QDoRA) is an area of active development, so expect tooling and performance to evolve.
When Should You Consider DoRA?
Based on my results and the broader literature, DoRA seems most compelling in these scenarios:
- When You’re Fighting for Every Parameter: DoRA often delivers comparable or superior performance at a significantly smaller rank
r. A DoRA run atr=8might match a LoRA run atr=16orr=32, which is a meaningful saving in trainable parameters and memory. - When You’re Tired of Babysitting Hyperparameters: If you find your LoRA results are brittle and overly sensitive to learning rate, dropout, or rank, DoRA’s decomposition may offer a more stable and forgiving training process.
- When Fine-Tuning Quantized Models: QDoRA is an attractive proposition for closing the quality gap sometimes seen with QLoRA, while maintaining a minimal memory footprint for deployment on resource-constrained hardware.
Conclusion
My experiments with DoRA on Mistral-7B have been compelling. Its theoretical foundation-decomposing weights into magnitude and direction-is elegant, and its implementation in PEFT makes it immediately accessible. While this elegance comes at the cost of training speed, the potential for superior performance at lower ranks and improved stability makes DoRA a powerful alternative to LoRA.
For my own projects, especially where parameter efficiency and robustness are paramount, I will be defaulting to DoRA more frequently. The core lesson remains: experiment relentlessly and find what works for your specific model, dataset, and constraints. And for the sake of your inference latency, always merge your adapter weights before deployment. The ecosystem around efficient fine-tuning is evolving at a breakneck pace; staying current is the only way to keep up.
Further Reading (updated)
For those who wish to dive deeper, these resources are invaluable:
- The Original DoRA Paper: Liu, S. Y., Lin, C.H., Lee, C.Y., & Wang, C.Y. (2024). DoRA: Weight-Decomposed Low-Rank Adaptation. arXiv:2402.09353.
- Sebastian Raschka’s Analysis: A superb conceptual overview in his “Ahead of AI” newsletter: Ahead of AI #13: From LoRA to DoRA & Fine-Tuning Mixtral on a Single GPU.
- PEFT Library Documentation: The official Hugging Face PEFT guide for LoRA and DoRA configurations.
- Answer.ai Blog on QDoRA with FSDP: An advanced post on using QDoRA in distributed training setups: Nearly SOTA Llama-3 8B Fine-tuning, Now on a Single GPU with FSDP and QDoRA.