Key Takeaways
- The brutal trade-off in quantization has always been speed versus accuracy. AutoRound carves out a new sweet spot, achieving the precision of expensive Quantization-Aware Training (QAT) with the speed of simple Post-Training Quantization (PTQ).
- The prize is tangible: 4-bit models produced by AutoRound retain near-FP16 accuracy while slashing model size by 8× and VRAM usage by roughly 4×. Suddenly, powerful models fit on hardware that isn’t a server farm.
- Pragmatism wins: This isn’t some bespoke, academic format. AutoRound checkpoints are compatible with the GPTQ ecosystem, meaning you can drop them straight into production workhorses like vLLM.
- This isn’t a week-long cluster affair. We’re talking hours on a single GPU. Llama-3 8B converts in about 90 minutes.
- Let’s be clear: 2-bit is still the wild frontier. Don’t expect production-ready magic here without turning the optimization dials way up or accepting a significant accuracy hit.
Technical Context: Why AutoRound for Low-Bit Quantization?
- AutoRound elevates quantization from a crude rounding exercise to a discrete optimization problem, sidestepping the precipitous accuracy cliff that plagues most PTQ methods below 4 bits.
- The secret sauce is SignSGD, which makes the optimization computationally cheap, allowing it to scale to billion-parameter models without requiring a data center.
- Compatibility is king. By aligning with the GPTQ format, AutoRound ensures its outputs aren’t just academic curiosities but deployable assets.
1. Why Do We Care About Low-Bit Quantisation?
The brutal physics of Large Language Models (LLMs) is that they are memory-bound. Every single parameter is a tax on your VRAM, a bottleneck for your memory bus. Shifting from 16-bit floating-point numbers to smaller -bit integers is the most direct way to slash this tax. It shrinks the model’s storage footprint, reduces memory bandwidth during inference, and ultimately translates to faster responses and lower cloud bills.
Weight-only PTQ methods like GPTQ or bits-and-bytes (BnB) gained traction because they’re simple and require no fine-tuning data. But they hit a wall. For most, 4-bit is the floor; go lower, and performance nosedives. AutoRound is an attempt to break through that floor.
2. A Primer on Weight Quantisation
For a given weight matrix and a scalar step size
, the game is to map each high-precision weight to a cramped integer space. With uniform symmetric quantisation, the mapping is:
The crucial decision is the rounding-that innocent-looking operator. Naïve round-to-nearest (RTN) treats each weight in isolation, ignoring the intricate web of correlations within the matrix. This disregard for the bigger picture is what hammers your model’s accuracy.
3. Enter Intel AutoRound
This is where AutoRound gets clever. Instead of treating rounding as a dumb, one-shot decision, it reframes it as a discrete optimization problem and brings a surprisingly lightweight tool to bear: Signed Stochastic Gradient Descent (SignSGD).
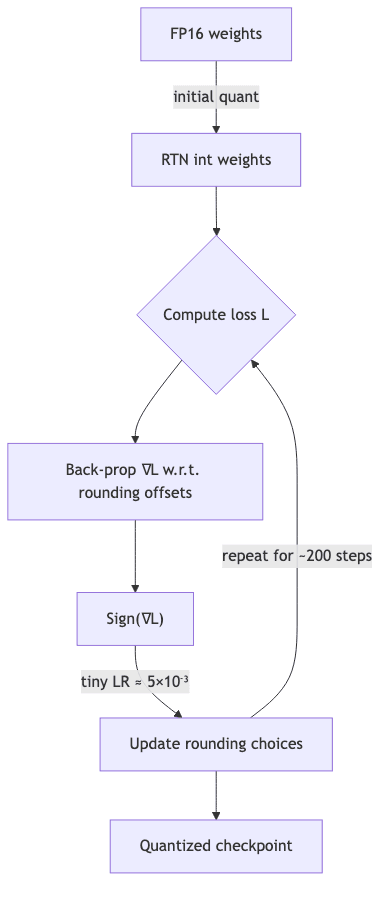
The algorithm is data-driven but not data-hungry. You feed it a few short, random text sequences. For each weight, the algorithm measures the impact on the loss if it were rounded up versus down. Then, it nudges the rounding choice (a binary decision, ±1) in the direction that lowers the loss. Using SignSGD means the gradients are just +1 or -1, making the optimization loop astonishingly fast.
4. Hands-On: Quantising Llama-3 8 B
Let’s get our hands dirty. The actual implementation is refreshingly straightforward.
from transformers import AutoModelForCausalLM, AutoTokenizer
from auto_round import AutoRound
import torch
model_name = "meta-llama/Meta-Llama-3-8B"
model = AutoModelForCausalLM.from_pretrained(model_name,
torch_dtype=torch.float16)
tok = AutoTokenizer.from_pretrained(model_name)
autoround = AutoRound(
model, tok,
bits=4, # 4-bit weights
group_size=128, # one scale per 128 values
seqlen=512, # SignSGD training length
batch_size=2,
gradient_accumulate_steps=4,
sym=False, # asymmetric quantisation
iters=200, # SignSGD steps
device="cuda"
)
autoround.quantize() # <≈1.5 h on a single A10>
autoround.save_quantized("./llama3-8b-4bit-autoround") # GPTQ-compatibleYou can experiment by swapping bits=2 or increasing iters. Using sym=True enables faster inference kernels like Marlin, if you’re willing to trade a sliver of accuracy for speed.
5. How Good Is the Result?
The numbers speak for themselves.
| Setting | Winogrande | HellaSwag | |
|---|---|---|---|
| FP16 baseline | 86.7 | 83.5 | |
| 4 bit AutoRound | 85.9 | 82.7 | Δ < 1.2 |
| 4 bit AutoGPTQ | 83.1 | 79.9 | |
| 4 bit BnB | 82.4 | 78.1 | |
| 2 bit AutoRound | 70 – 74 | 60 – 63 | ⇣ |
*Numbers averaged over zero-shot runs with
lm-eval-harness.*
The takeaway: At 4-bit, the accuracy drop is almost a rounding error, handily beating other popular PTQ methods. But look at 2-bit. That’s a cliff, not a curve. It’s a stark reminder that there’s no free lunch, at least not without more work-like cranking up the optimization steps or bringing in other techniques.
6. Performance & Memory Footprint
The payoff is immediate and tangible.
- GPU RAM: A 4-bit quantized 8B model uses ~⅛ the memory of its FP16 counterpart. It fits comfortably on a 12 GB consumer GPU.
- CPU RAM during quantization: Be prepared. AutoRound needs to hold the full-precision model in memory plus buffers, so keep ~32 GB of system RAM free.
- Throughput: Benchmarked in vLLM, 4-bit AutoRound is neck-and-neck with 4-bit GPTQ (within 1%) and delivers around 1.9× the throughput of the FP16 baseline.
7. Recipes & Hyper-Parameters
The defaults are sane, but for those of us who like to tinker under the hood, here are the key levers to pull.
| Hyper-parameter | Rule-of-thumb |
|---|---|
bits |
4 for production; 2 for research/edge devices |
group_size |
64 or 128; smaller → better accuracy, larger → smaller model |
iters |
200 is fine for 4-bit; push to 1k–2k for 2-bit |
sym |
True for Marlin kernel speedups; False for best quality |
iters0 |
At least 512, ideally matching the model’s context length |
iters1 |
Crank it up to saturate your GPU, but don’t hit OOM |
8. Limitations & Open Questions
This isn’t a silver bullet. It’s important to understand the boundaries of the art.
- Activations are untouched. This is weight-only quantization. The other half of the memory problem-activations-remains a separate challenge.
- Giant models (70B+) can still be a headache. The quantization process itself might exceed the RAM of a typical workstation, pushing you back into multi-GPU territory.
- The 2-bit gap feels like a problem begging for a hybrid solution. The sensitivity to rounding noise suggests that a small, QLoRA-style fine-tune after quantization could be the missing piece to close the performance gap.
- Compatibility can be tricky. Older GPTQ loaders might stumble on the asymmetric scales AutoRound can produce. When in doubt, stick to the native
iters2 loading format or enforceiters3 for maximum compatibility.
9. Conclusion
I’m genuinely impressed. It’s rare that a new technique lands so perfectly in the sweet spot between academic purity and engineering pragmatism. AutoRound does. It gives us near-QAT accuracy at PTQ speeds, packaged in a format that plugs directly into the tools we already use. The barrier to deploying a multi-billion parameter model in high-fidelity 4-bit has been dramatically lowered.
While the bleeding edge of 1- and 2-bit quantization remains a frontier for research, the 4-bit method is solid, practical, and production-ready.
Give it a spin. Measure it on your workloads. And see how far down the bit-depth rabbit hole you’re willing to go.
Further reading:
- AutoRound paper: https://arxiv.org/abs/2309.05516
- AutoRound source: https://github.com/intel/auto-round
- Marlin 4-bit kernels: https://github.com/IST-DASLab/marlin
Happy quantising