Scaling Language Models Without Matrix Multiplication

A Different Kind of Math

Deep learning, for all its abstract sophistication, runs on a surprisingly brutish engine: matrix multiplication. We’ve become so accustomed to its dominance that challenging it feels like questioning gravity. The entire ecosystem, from CUDA cores to research papers, is built around making this one operation faster.

But what if this is a local optimum? What if the path to truly efficient, scalable intelligence isn’t paved with more FLOPs, but with a different kind of math entirely?

This is the premise of MatMul-free LM. It’s not an incremental tweak; it’s a radical reimagining of the core computational primitives.

The MatMul‑free LM: An architecture that jettisons all $\mathbf{W}\mathbf{x}$ products, yet holds its own against Transformer-style models up to 2.7B parameters.
BitLinear’s Radical Diet: Weights are quantized to $\{-1,0,1\}$ , activations to 8-bit. The dense layer collapses into a flurry of signed additions, not multiplications.
Attention is All You… Don’t Need?: A MatMul‑free Linear GRU (MLGRU) replaces self-attention, using element-wise products and gating to capture long-range context without the quadratic overhead.
Brutal Efficiency: Fused CUDA kernels and Triton code deliver 25–60% memory savings and a 4–5× inference speed-up. A prototype FPGA runs a 13B model on the power of a laptop charger (13W).
Favorable Scaling Laws: The performance gap to full-precision Transformers appears to narrow with scale. Efficiency doesn’t just happen; it improves as you get bigger.

Why Remove MatMul?

Matrix multiplication is the energy-guzzling, memory-choking tyrant of deep learning. Modern GPUs dedicate vast tracts of silicon to their matrix-multiply-accumulate (MMA) units. To move forward, sometimes you must question the foundation. Excising MatMul promises a few rather attractive outcomes:

Slash power draw: Additions cost roughly 3× less energy than multiplies on a 7nm node. Physics is unforgiving, but it can be on your side.
Shrink memory bandwidth: Ternary weights can be packed into 2 bits, a stark contrast to the 16 bits of FP16. This isn’t an incremental improvement; it’s a phase shift in data density.
Simplify the silicon: Moving to add-only primitives opens the door to lean, specialized ASIC/FPGA accelerators that don’t need the complexity of a full MMA.

Previous attempts, like AdderNet or BitNet, nibbled at the edges, removing multiplications in some layers. The MatMul-free LM is the first to go all the way, taking the gospel of addition-only to scale and proving it works beyond the 1B parameter mark.

Building Blocks

1. BitLinear Layer

The foundation of the MatMul-free world is the BitLinear layer. It takes the canonical dense layer:

$\mathbf{y}=\mathbf{W}\mathbf{x}+\mathbf{b}$

and puts it on a radical diet. The weight matrix $\mathbf{W}$ is aggressively quantized, with each element $W_{ij}$ forced into the set $\{-1, 0, 1\}$ . The dot product $w\_{ij} x_{j}$ suddenly becomes a choice: {−x, 0, +x}. The multiplication evaporates, replaced by a conditional addition/subtraction or a skip. The logic is brutal and effective.

The forward pass here uses a Straight-Through Estimator (STE) during backpropagation; the w_q = self.weight.sign() is the hard quantization for the forward pass, but the gradients flow back to the full-precision self.weight, allowing the network to learn.

class BitLinear(nn.Module):
    """Ternary weight, int8 activation linear layer (training‑time fake‑quant)."""
    def __init__(self, in_features, out_features, bias=False):
        super().__init__()
        self.weight = nn.Parameter(torch.empty(out_features, in_features))
        nn.init.uniform_(self.weight, -1, 1)  # initial real‑valued weights
        self.bias = nn.Parameter(torch.zeros(out_features)) if bias else None

    def forward(self, x):
        # STE: straight-through-estimator used in back-prop
        w_q = self.weight.sign() + (self.weight - self.weight.detach())
        x_q = torch.clamp((x * 127).round(), -128, 127)
        # F.linear is still used but kernel expands to add/sub due to ternary w_q
        return F.linear(x_q.float(), w_q, self.bias)

Note The repo provides an optimised Triton kernel FusedBitLinear that packs four ternary weights per int8 and fuses layer‑norm + activation for speed.

2. MatMul‑free Linear GRU (MLGRU)

Here, self-attention-the celebrated engine of the Transformer-is shown the door. In its place comes a MatMul‑free Linear GRU (MLGRU), an MLP-style recurrent block that leans on element-wise Hadamard products. It captures long-range dependencies without the crushing $\mathbf{QK}^\top$ computation.

$\begin{aligned} \mathbf{u}_{t} &= \sigma\big(\mathrm{LN}(\mathbf{x}_{t})\big)\\ \mathbf{h}_{t} &= (1-\mathbf{u}_{t})\odot\mathbf{h}_{t-1}+\mathbf{u}_{t}\odot\mathrm{SiLU}\big(\mathrm{LN}(\mathbf{x}_{t})\big) \end{aligned}$

The only learnable parameters live in the BitLinear projections inside the RMSNorm and SiLU blocks. No quadratic attention scores are ever required.

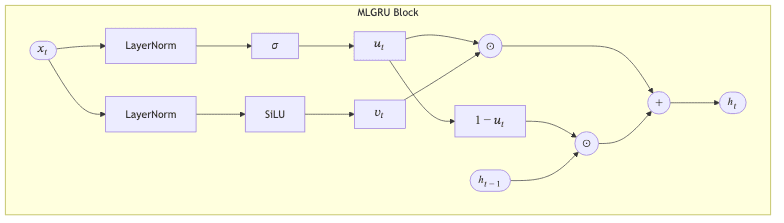
3. MatMul‑free GLU (MGLU)

The feed-forward network follows the same philosophy. It’s a Gated Linear Unit (GLU), but its projections are BitLinear layers. The mixing is done element-wise. No matrix multiplications hide in the shadows here either.

Results at a Glance

So, does this computational austerity actually work? The numbers suggest it’s more than a curiosity. While it doesn’t uniformly beat a state-of-the-art Transformer++, the gap is surprisingly narrow-and in some cases, it closes as the model scales.

Model	Params	Tokens Trained	ARCe	ARCc	HellaSwag	Open‑QA (OQ)	PIQA (PQ)	WinoGrande	Avg.
Transformer++	370 M	15 B	45.0	24.0	34.3	29.2	64.0	49.9	41.1
MatMul‑free RWKV‑4	370 M	15 B	44.7	22.8	31.6	27.8	63.0	50.3	40.0
Ours (MM‑free LM)	370 M	15 B	42.6	23.8	32.8	28.4	63.0	49.2	40.3
Transformer++	1.3 B	100 B	54.1	27.1	49.3	32.4	70.3	54.9	48.0
Ours (MM‑free LM)	1.3 B	100 B	54.0	25.9	44.9	31.4	68.4	52.4	46.2
Transformer++	2.7 B	100 B	59.7	27.4	54.2	34.4	72.5	56.2	50.7
Ours (MM‑free LM)	2.7 B	100 B	58.5	29.7	52.3	35.4	71.1	52.1	49.9

(Zero‑shot accuracy; higher is better)

Quick‑start with the GitHub Code

Talk is cheap. The authors provide a direct path for getting your hands dirty. The model is available on Hugging Face and can be pulled down with a few lines of code:

pip install -U git+https://github.com/ridgerchu/matmulfreellm

import os
os.environ["TOKENIZERS_PARALLELISM"] = "false"

from mmfreelm.models import HGRNBitConfig
from transformers import AutoModelForCausalLM, AutoTokenizer

# 1️⃣ Build a random‑initialised model (for finetuning experiments)
model = AutoModelForCausalLM.from_config(HGRNBitConfig()).cuda().half()

# 2️⃣ Or load a published checkpoint (replace with the actual HF repo name)
ckpt = "ridgerchu/mmfree-370m"
tokenizer = AutoTokenizer.from_pretrained(ckpt)
model = AutoModelForCausalLM.from_pretrained(ckpt).cuda().half()

prompt = "In a shocking finding, scientists discovered a herd of unicorns living in a remote "
inputs = tokenizer(prompt, return_tensors="pt").to(model.device)
outputs = model.generate(**inputs, max_length=32, do_sample=True, top_p=0.4, temperature=0.6)
print(tokenizer.decode(outputs[0], skip_special_tokens=True))

Training Tips

When using the custom Triton kernels, set TORCH_CPP_LOG_LEVEL=INFO TORCH_DYNAMO_DISABLE=1 to avoid unnecessary noise.
The authors’ pretraining recipe is aggressive: a T=32k sequence length, AdamW (β=(0.9,0.95)), and a cosine learning rate schedule peaking at 2e‑4 for the 2.7B model.
Don’t skip on activation recomputation. The memory savings from ternary weights have a compounding effect here. It’s a critical lever for fitting larger models into the same VRAM budget.

Hardware Speed‑ups

This is where the architectural purity pays dividends. The fused Triton kernels aren’t just a minor optimization:

Training 25.6 % faster, 61 % lower GPU memory vs. naïve PyTorch.
Inference 4.57 × latency improvement, 10 × memory cut for the 13 B model.

The FPGA prototype is perhaps the most telling result. It runs the 13B model at 13W and a respectable 40 tokens/s. That’s the power budget of a laptop charger. Let that sink in.

Final Thoughts

MatMul-free LM is more than just an efficiency play; it’s a philosophical statement. It suggests that our relentless pursuit of bigger, faster matrix multiplication units might be a form of computational brute force, a costly substitute for more intelligent algorithmic design. The primacy of the ‘how’-the raw FLOPs-has overshadowed the ‘what’ and ‘why’ of the computation itself.

This work demonstrates that we can embed significant computational savings directly into the architecture. By trading multiplications for additions and embracing aggressive quantization, we don’t just reduce energy consumption; we change the hardware requirements fundamentally. This is how you escape the gravitational pull of ever-larger GPUs and open a path to powerful, on-device intelligence that doesn’t melt the battery.

While the accuracy still trails the top-tier, full-precision Transformers, the scaling laws are promising. The gap narrows. This isn’t the end of the road for MatMul, but it might be the beginning of its dethronement as the undisputed king of deep learning. The future may belong to those who build with thriftier primitives, proving that true performance comes from elegance, not just force.

Posted in AI / ML, LLM Advanced by Rakshit Kalra