Key Takeaways
- MCT Self-Refine (MCTSr) elevates a commodity 8-billion-parameter LLaMA-3 model into a reasoning engine that challenges GPT-4 on Olympiad-level mathematics.
- The method fuses Monte-Carlo Tree Search with self-refinement and self-rewarding prompts, building a search tree over partial solutions rather than discrete game states.
- This allows the infinite branching factor of LLM reasoning to be intelligently pruned using an Upper-Confidence bound (UCT), turning unstructured generation into a guided search.
- The implementation is open-source, refreshingly minimal, and runs on standard vLLM servers without proprietary machinery.
- With just eight roll-outs, the method doubles the success rate over vanilla Chain-of-Thought on hard math problems and pushes LLaMA-3 8B past 90% on GSM8K.
- MCTSr is a generalizable framework: swap the reward function, and it becomes a template for alignment, black-box optimization, or agentic planning.
1. Why This Matters
We’ve seen LLMs exhibit flashes of emergent brilliance, yet even formidable models can stumble on grade-school arithmetic-a frustrating paradox. The core problem is the lack of structured, iterative reasoning. Zhang et al. pose a fundamental question: can classical search techniques grant a small model the cognitive depth of a larger one, much as AlphaGo amplified Monte-Carlo search?
Their answer, MCT Self-Refine, is an elegant synthesis that sidesteps fine-tuning entirely. In a landscape dominated by talk of massive, opaque models and gargantuan RLHF budgets, this paper is a welcome dose of first-principles thinking. It’s a testament to the enduring power of marrying clever prompting with the established logic of statistical search.
2. The Algorithm Distilled
2.1 The MCTS Foundation
Monte-Carlo Tree Search (MCTS) navigates vast possibility spaces by iteratively building a search tree. It cycles through four phases: selection, expansion, simulation, and back-propagation. The lynchpin is the UCT score, which elegantly balances exploiting known good paths with exploring uncertain ones:
Here, is the average reward of node
,
is its visit count, and
is the total visits to its parent. It’s a battle-tested heuristic for finding signal in immense noise.
2.2 What MCTSr Adds
MCTSr adapts this logic from game states to the abstract space of “solutions.”
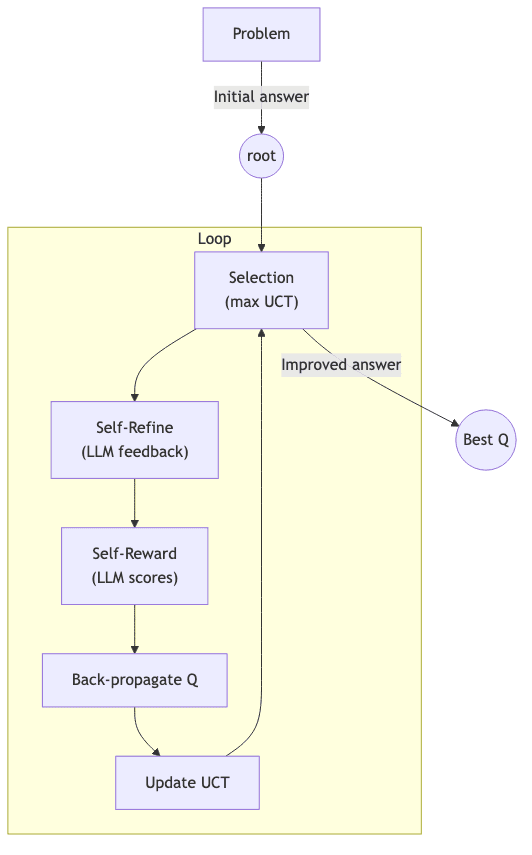
- Selection: Traverse the tree by greedily picking the node with the highest UCT score until a leaf is reached.
- Self-Refine: Force the LLM to act as its own ruthless critic, generating feedback on the leaf node’s answer. It then regenerates the solution conditioned on this critique.
- Self-Evaluation: The model scores its own refined attempt on a scale of [–100, 100]. This self-reward signal is sharpened with simple heuristics (like disallowing perfect scores) to prevent score inflation and maintain a useful distribution.
- Back-propagation: A node’s value,
, is updated as the mean of its (worst reward, average reward, and best child’s reward), propagating the new information up the tree.
- UCT Update & Pruning: The search intelligently curtails expansion. A branch is pruned once its visit count hits a cap and one of its children has a better score than the parent. This prevents the tree from becoming unwieldy in an unbounded action space.
The process terminates after a fixed number of roll-outs or if the solution quality stagnates.
2.3 The Core Logic
The implementation is surprisingly direct. Here is the essence in pseudo-python:
from llm import llama3_instruct as llm
from mcts import Node, uct_select
def mctsr(problem, rollouts=8):
root = Node(initial_answer(llm, problem))
for _ in range(rollouts):
leaf = uct_select(root)
critique = llm.reflect(problem, leaf.answer)
child_ans = llm.refine(problem, leaf.answer, critique)
reward = llm.score(problem, child_ans)
leaf.add_child(child_ans, reward)
leaf.backprop()
return root.best_answer()(The full, working implementation is available in the cited GitHub repository.)
3. Experimental Highlights
The results speak for themselves. The performance gains are not marginal; they are substantial, particularly on problems requiring longer chains of reasoning where iterative feedback has the most impact.
| Dataset | Metric | Zero‑Shot CoT | Self‑Refine | MCTSr 4‑roll | MCTSr 8‑roll |
|---|---|---|---|---|---|
| GSM8K | Acc. % | 74.1 | 87.0 | 93.0 | 96.7 |
| GSM‑Hard | Acc. % | 25.5 | 33.4 | 39.9 | 45.5 |
| MATH (overall) | Acc. % | 24.4 | 35.7 | 47.1 | 58.2 |
| Math Odyssey | Acc. % | 17.2 | 30.3 | 40.1 | 49.4 |
Remarkably, these gains are achieved without any gradient updates. Against closed-source giants, a model 15× smaller running MCTSr closes the gap on GPT-4-Turbo for GSM8K and halves the deficit on Olympiad-level benchmarks.
4. Strengths & Lingering Questions
| 👍 Strengths | ⚠️ Lingering Questions |
|---|---|
| Pure Prompting: No training budget or GPUs required. | Heuristic Reward: Self-reward is clever but prone to anchor bias, potentially penalizing creative but non-obvious solutions. |
| Model-Agnostic: Works with any capable open-source LLM. | Latency Cost: Eight roll-outs imply an ≈8× latency hit, making it unsuited for interactive use without further optimization. |
| Concise Codebase: The implementation is clear and vLLM-friendly. | Memory Growth: The tree can grow quadratically with roll-outs if all branches are retained, posing a memory challenge. |
| Clear Ablations: The paper rigorously isolates the effect of each component. | Outdated Comparisons: The work doesn’t benchmark against more recent reward-model-driven search methods like MC-Nest (2024). |
5. My Perspective & Future Directions
MCTSr is not an end-point but a powerful primitive. I see several immediate paths for extension:
- Decouple the Reward Model: Replacing self-reward with a specialized, fine-tuned verifier (like a Rubric LLM) would provide a more objective and robust signal, moving beyond the model’s own biases.
- Hybrid Search: Combine beam search for the initial, high-confidence steps of a solution, then deploy MCTS to explore the more ambiguous or difficult branches.
- Dynamic Roll-outs: Instead of a fixed budget, dynamically increase the number of roll-outs only when the tree’s value function begins to plateau, allocating compute where it’s most needed.
- Generalize the Framework: The core insight-that a “solution” can be a “state” in a search tree-is incredibly general. Code generation, automated theorem proving, and even complex planning are obvious next domains.
The real test of its efficiency will be porting it to a minimal backend like Phi-3-mini. I have an inkling it could tackle introductory CS proofs on something as constrained as a Raspberry Pi-a true test of squeezing intelligence from commodity hardware.
6. Conclusion
MCT Self-Refine is a powerful demonstration that intelligence isn’t just about scale; it’s about structure. By layering deliberate feedback loops and guided search atop a competent base model, we can forge sophisticated reasoning capabilities from commodity components. It proves that sometimes, the most effective way to make a model smarter is simply to force it to think twice. The architecture of thought matters.