Introduction
The narrative in AI often pits the stochastic, creative chaos of large language models against the rigid, brittle world of formal logic. The interesting work, as usual, happens at the messy intersection. Google DeepMind’s original AlphaGeometry was a notable foray into this space, solving an impressive number of International Mathematical Olympiad (IMO) geometry problems. But it was a promising, if flawed, first attempt.
Its successor, AlphaGeometry 2 (AG2), is something else entirely. It has shifted the goalposts, cracking a staggering 84% of IMO geometry problems from the last quarter-century. For the first time, a machine is outperforming the average human gold medallist. This isn’t just a bigger model; it’s a better-designed machine. I’ll unpack how AG2 achieves this, why its architecture matters more than its components, and where this trajectory leads.
Key Takeaways
- Human-beating performance: AG2 solves 84% of IMO geometry problems (2000–2024), reaching a capability level beyond the average IMO gold medallist.
- A richer language for thought: The system’s internal language was expanded to cover 88% of problem types, including those with loci and linear relations.
- A 200× faster symbolic engine: A C++ rewrite and smarter algorithms make the symbolic core brutally efficient. The grunt work still matters.
- A specialised LLM for creative leaps: A Gemini-based Mixture-of-Experts model, trained on 300M synthetic theorems, provides the intuitive sparks.
- Collaborative search: A team of AI agents searches in parallel, sharing discoveries to find proofs a lone genius would miss.
- Closing the gap: Automated translation from natural language and diagrams into formal code removes a key human bottleneck.
A Quick Recap of AlphaGeometry 1
The original system was an elegant fusion: a transformer model (trained on 100M synthetic proofs) proposed creative auxiliary points, and a deduction engine called DDAR 1 verified if those points led to a proof. While clever, AG1 hit three predictable architectural ceilings:
- Limited Language: It couldn’t express concepts like moving points (loci) or complex ratios.
- Slow Deduction: The symbolic engine was painstakingly slow, hobbled by polynomial and exponential search complexities.
- Shallow Search: Its single-minded beam search was prone to getting stuck in local, unpromising rabbit holes.
AG2 systematically demolishes each of these ceilings.
What’s New in AlphaGeometry 2?
1. A More Expressive Geometry DSL
You can’t reason about concepts you can’t name. AG2’s domain-specific language is upgraded with new predicates like acompute, distmeq, and templates for loci (e.g., “point moves on a circle through X”). This gives the machine the vocabulary to reason about dynamic problems, angle sums, and ratios, boosting its coverage of IMO problem statements from a respectable 66% to a commanding 88%.
2. Automated Formalisation & Diagram Generation
Manual translation was the unglamorous, artisanal bottleneck in AG1. AG2 automates it. Gemini 1.5 is prompted with a few examples to directly translate natural-language problems into formal AG code. A sophisticated three-stage optimiser then constructs a valid, non-degenerate diagram-first sampling, then refining with gradient descent and Gauss-Newton methods-all without a human needing to sketch a thing.
3. DDAR 2 – Faster, Stronger, Smarter
This is about brute-force engineering making the ‘impossible’ search space tractable.
- Double-point reasoning: DDAR 2 grasps an intuition human geometers use constantly: that points derived from different constructions might actually be the same. This allows for clever reformulations and shortcuts.
- Algorithmic pruning: Smarter algorithms for detecting similar triangles and cyclic quadrilaterals slash complexity from a crippling
to a manageable near-cubic time.
- C++ core: The core Gauss elimination routine was rewritten from Python into C++, exposed via pybind. The result? A >300× reduction in runtime on hard problems.
# Benchmarked speed-up (25 tough IMOs, 50 runs)
DDAR 1 ➜ 1179.6 s ± 8.0
DDAR 2 ➜ 3.45 s ± 0.054. Bigger & Smarter Synthetic Data
The solution to needing more creativity? Generate a synthetic universe of problems to learn from. AG2’s data generation pipeline was scaled to create diagrams twice as large and proofs ten times longer. A greedy algorithm replaces exponential-time proof minimisation with linear passes, ensuring the data firehose could keep up with the system’s larger appetite.
5. Gemini-Based LLM & Multi-Modal Flair
Instead of building a bespoke model from scratch, AG2 fine-tunes existing Gemini checkpoints. The team found that details like the tokenizer barely impacted performance-a classic lesson in not over-optimizing the wrong component. A multi-modal variant can even ingest diagrams as images, though the visual input served more to add diversity to the search than to improve raw accuracy. Pragmatism over purity.
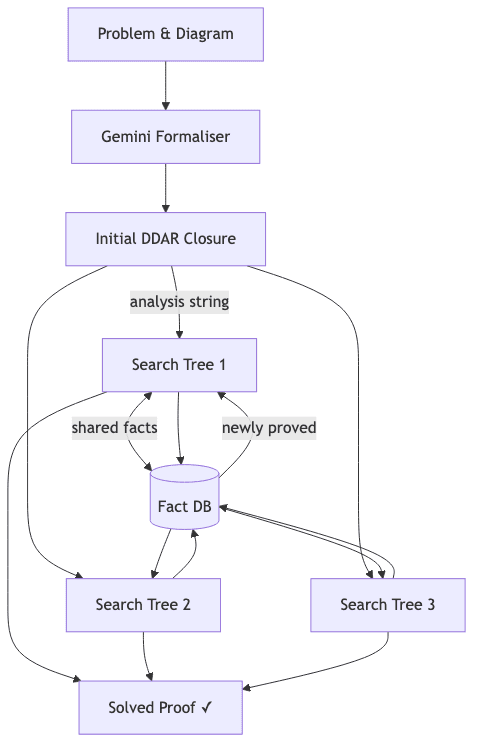
6. SKEST – Collaborative Tree Search
This is perhaps the most elegant architectural idea in the system. Instead of one monolithic search, AG2 fields a team of search agents (depth-first, breadth-first, etc.) that explore the problem space in parallel. When one agent proves a new fact, it writes it to a shared database, which instantly becomes available to all other agents, “fertilising” their own explorations. It’s a system designed to weaponize serendipity.
Benchmarks & Results
| Metric | AlphaGeometry 1 | AlphaGeometry 2 |
|---|---|---|
| IMO 2000‑24 solve-rate | 54% | 84% |
| Coverage of problem statements | 66% | 88% |
| Pure symbolic (no LM) | 14 / 50 | 16 / 50 |
| Time per hard DDAR run | ~1180 s | 3.45 s |
More tellingly, AG2 solved 20 of the 30 hardest IMO shortlist problems-those deemed too difficult for the final competition. This is a domain where even elite human specialists often get stuck.
A Quick Test-Drive
Don’t just take my word for it. While full-scale inference requires serious hardware, the team has open-sourced the code, allowing you to run the DDAR 2 engine and smaller models locally.
# Clone the public repository (MIT-licensed)
git clone https://github.com/google-deepmind/alphageometry.git
cd alphageometry
# Set up an isolated environment
python3 -m venv .venv
source .venv/bin/activate
pip install --require-hashes -r requirements.txt
# Download lightweight weights & vocab (~2 GB)
./download.sh --preset=small
# Solve a classic Olympiad geometry problem
python run.py --problem examples/IMO2004_P1.agWhy This Matters
- Bridging formal and informal mathematics – Auto-formalisation is a meaningful step toward closing the chasm between informal human math and formal, machine-verifiable proofs. It’s essential scaffolding for any future “research co-pilot.”
- Search as a differentiator – SKEST proves, yet again, that system architecture can trump sheer component horsepower. A clever system orchestrating multiple agents can discover paths a single, more powerful agent would miss.
- The blueprint for hybrid AI – This is the model. The LLM provides creative, often messy, hypotheses. The symbolic core provides unforgiving, logical validation. One without the other is either ungrounded or uninspired.
Limitations & Future Directions
- Blind spots remain. The system is still blind to entire classes of problems involving inequalities or variable points, as it lacks support for non-linear constraints.
- The hardware appetite is immense. Full-scale runs depend on TPUv4 pods. Community forks like AG for Masses are already working on more accessible CPU implementations, but this highlights the resource barrier.
- Proofs can still be brittle. While the engine guarantees correctness, generating end-to-end human-readable proofs without the DDAR verifier remains a frontier.
Future work will likely integrate concepts like projective geometry and inversion, perhaps using reinforcement learning to guide the search for sub-goals. 100% IMO coverage is no longer a fantasy.
Closing Thoughts
Reading the AG2 paper felt like watching the final pieces of a decade-long puzzle click into place. By systematically expanding the system’s language, brutally accelerating its deductive engine, and creating a framework for its internal agents to collaborate, AlphaGeometry 2 doesn’t just inch ahead-it makes a decisive leap. It’s a testament to systems thinking.
For anyone tracking the progress of AI reasoning, automated theorem proving, or simply beautiful mathematics, AG2 is both a milestone and a clear roadmap for what comes next.