Magistral – Scaling Reasoning with Efficient GRPO Training

Key Takeaways

RL Alone Does The Heavy Lifting – Training Mistral Medium with Group Relative Policy Optimisation (GRPO) alone catapults AIME‑24 pass@1 from a dismal 26% to a formidable 74%. No reasoning traces required.
The Devil’s in the GRPO Details – This isn’t your textbook PPO. Killing the KL penalty, normalizing loss across all tokens, and deploying asymmetric clipping (ε_high) are the keys to unlocking exploration.
The Real Lever is Length – The data is unambiguous: average reward scales with the logarithm of sequence length. The primary driver of success is encouraging the model to think longer.
Multimodality Gets a Free Ride – The startling bonus: RL training on text alone spontaneously improved multimodal MMMU scores by 5%. The vision encoder simply came along for the ride.
Distillation Still Pays Dividends – A 24B student model, first distilled from the RL parent and then put through its own RL boot camp, grabs another 5-10 points.

Why I Care

Large language models are masters of surface-level fluency and masters of brittle failure when confronted with problems requiring genuine reasoning. The default state is confident nonsense. When DeepSeek-R1 demonstrated that reinforcement learning from verifiable rewards (RLVR) could effectively mass-produce reasoning, it was a signal. But it left a critical question unanswered: how far can you push pure reinforcement learning, stripped of the crutch of supervised fine-tuning on human-written traces?

Mistral’s Magistral report delivered the answer. It’s a case study in disciplined, industrial-scale RL.

Here, I’m dissecting the paper, their public notes, and the code. I’ll fill in some of the gaps and reflect on what this means for anyone actually trying to build systems that need to think.

A Minimal Recap of GRPO

GRPO is PPO stripped for combat. It’s PPO without a critic. For each prompt, you sample G completions, assign a binary reward, and use the group’s performance as the baseline. The original objective is:

$\mathit{J}(\theta)= \mathbf{E}_{q, \{o_{i}\}} \sum_{i=1}^{G}\sum_{t=1}^{|o_{i}|} \frac{1}{|o_{i}|} \operatorname{clip}\Bigg(\frac{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_\textrm{old}}(o_{i,t}|q,o_{i,<t})}, 1-\varepsilon,1+\varepsilon\Bigg) \hat A_{i}$

with the advantage $\hat A_{i} = (r_{i}-\mu)/\sigma$ .

Magistral’s version is leaner and meaner:

$\mathit{J}_{\textrm{Mag}}(\theta)= \frac{1}{\sum_{i} |o_{i}|} \sum_{i,t} \operatorname{clip}\Bigg(\frac{\pi_{\theta}}{\pi_{\theta_\textrm{old}}}, 1-\varepsilon_{\textrm{low}}, 1+\varepsilon_{\textrm{high}}\Bigg) \hat A^{\textrm{norm}}_{i}.$

The critical mutations: the KL term vanishes. Gone. Groups where every sample is either correct or incorrect? Discarded, as they offer no gradient. This isn’t academic tinkering; it’s pragmatic engineering.

The Four Pillars of a Good Reward Signal

Axis	Implementation	Rationale
Formatting	Strict gates on `<think>` / `</think>`, `\boxed{}`, and fenced code.	To ensure the machine can grade its own homework without ambiguity.
Correctness	SymPy for math equivalence; compile-and-run 20 tests for code.	A clean, binary signal. No partial credit for being ‘almost’ right. The reward is 0 or 0.9.
Length	Soft penalty only when l > l_max − l_cache.	To let the model think without letting it ramble into infinity.
Language Consistency	10% of prompts translated from English; fastText check on output.	Because a model that switches languages mid-thought feels schizophrenic, not intelligent.

The Asynchronous Beast: Engineering for Throughput

My reconstruction of Mistral’s architecture reveals a system obsessed with efficiency.

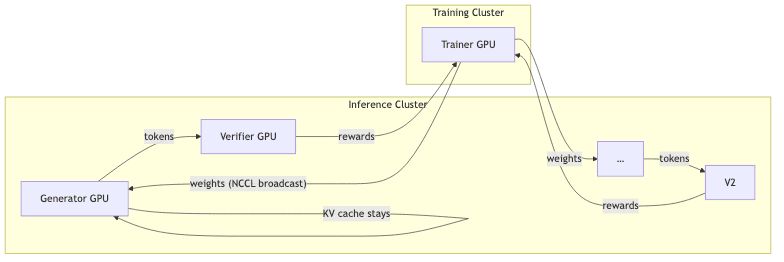
Generators are perpetual motion machines; they stream completions without waiting for weight updates.
The KV-cache is sacrosanct. It is not recomputed after a weight push. GRPO’s off-policy correction is robust enough to swallow the mismatch. Wasting cycles here is a cardinal sin.
Batches are driven by sequence count (2k–8k samples), then greedily packed. This slashes padding waste by 19%-a simple, effective trick for heavy-tailed sequence lengths.

This architecture confirms a core belief of mine: once you’ve tamed variance, raw throughput beats slavish on-policyness every single time.

What the Numbers Say

Pure RL on Mistral Medium

Benchmark	Base	Magistral Medium	Δ
AIME‑24 pass@1	26.8%	73.6%	▲ 46.8 pp
LiveCodeBench v5	29.1%	59.4%	▲ 30.3 pp
GPQA	59.6%	70.8%	▲ 11.2 pp

These aren’t mere incremental gains. This is what a well-oiled RL machine looks like when it’s firing on all cylinders.

The Small Model Story

SFT Only: Supervised fine-tuning on the teacher’s reasoning traces gets you to a respectable 65% on AIME. A solid baseline.
RL Only: Starting from scratch, pure RL lands in the same ballpark, though it struggles more with code generation. It’s a rougher ride.
SFT + RL: This is the real win. First, distill the teacher’s wisdom via SFT. Then, sharpen it with RL’s discipline. The result: 71% on AIME and the best overall performance.

The lesson is clear: distill if you have the data, but RL will always be there to squeeze out the last drops of performance.

Length is the Secret Sauce

Dig into the supplementary material, and you find the ghost in the machine. A principal component analysis of the weight trajectory reveals an axis that correlates almost perfectly with average sequence length. A plot of raw reward against length shows a nearly linear trend on a log-x scale.

This is the signature of a system where each incremental step of reasoning, however small, adds positive, if diminishing, marginal value.

Quickstart – Running Magistral Locally

To get your hands dirty, the recipe is simple:

from transformers import AutoTokenizer, AutoModelForCausalLM, TextStreamer

tokenizer = AutoTokenizer.from_pretrained("mistralai/Magistral-Small-2506", use_fast=True)
model     = AutoModelForCausalLM.from_pretrained(
    "mistralai/Magistral-Small-2506",
    torch_dtype="auto",
    device_map="auto",
)

prompt = "Solve 12x – 7 = 5x + 14."
msg = (
    "A user will ask you to solve a task. You should first draft your thinking process…\n"
    f"Problem:\n\n{prompt}"
)
inputs     = tokenizer(msg, return_tensors="pt").to(model.device)
streamer   = TextStreamer(tokenizer)
model.generate(**inputs, max_new_tokens=512, streamer=streamer, temperature=0.7)

The team exposed their GRPO trainer in the repo. To replicate their core finding, you just need to tweak the knobs: set KL_COEF=0 and tune EPS_HIGH to around 0.28. The magic is in the asymmetry.

What Failed (and Why I’m Glad It Did)

This is the kind of intellectual honesty that accelerates a field. The failures are often more instructive than the successes, and the Mistral team had the discipline to document them.

Entropy Bonus: An explicit term was too unstable. It either caused the model to collapse on math problems or explode on mixed data. The fix? Simply widening the asymmetric clipping range (ε_high) provided the stability the bonus couldn’t.
Partial Rewards for Code: Giving partial credit for passing some, but not all, unit tests feels principled. In practice, the noise drowned out the signal, hurting performance on LiveCodeBench by ~2 points. Binary is better.

Implications for Practitioners

Your reward signal lives and dies by sequence length. If your average length flatlines, your model has stopped thinking. Raise the limits or redesign the prompt.
Ditch the reference model. It’s a memory hog. Use the saved VRAM to double your batch size. You can thank me later.
When your sequences have fat tails, token-based batching is a fool’s game. Pack by sequence count to minimize padding waste.
Fear idle GPUs more than you fear asynchronous updates. The empirical bias is a ghost; the throughput gains are real.

Closing Thoughts

Magistral is a proof-of-concept for lean, industrial-scale reinforcement learning. It demonstrates that with disciplined reward shaping and pragmatic engineering, RL can be a brutally effective tool for scaling reasoning.

I’ll bet that asymmetric clipping and normalizing loss by token count, not sequence, become the default settings in any serious open-source RLHF stack within a year.

For my own work on an agentic math solver, the path is clear: a higher ε_high, enforced <think> blocks, and a reward function that logarithmically encourages deeper thought. I’ll be sharing the results.

Happy hacking! – RK (https://twitter.com/ra\_kalra)

Posted in AI / ML, LLM Intermediate by Rakshit Kalra