Harnessing the Universal Geometry of Embeddings

Key Takeaways

Vec2Vec learns a universal latent space that aligns embeddings from radically different models without needing paired examples.
The method outperforms optimal–assignment baselines and even bridges text–only models with multimodal encoders such as CLIP.
Successful translation lets attackers (or auditors!) recover sensitive attributes-or entire documents-from supposedly anonymised vector stores.
Cycle‑consistency, adversarial training, and a clever Vector‑Space‑Preservation loss are the secret sauce that keeps geometry intact.
Open‑source code is available on GitHub (rjha18/vec2vec), making it straightforward to experiment or reproduce the paper’s results.

1 Why Should I Care About Embedding Translation?

The original sin of every Retrieval‑Augmented Generation (RAG) pipeline is vector lock‑in. Once you commit to an embedding model, its coordinate system becomes your prison. Every downstream component, every ANN index, every persisted store is shackled to that specific geometric worldview. Migrating to a superior encoder has meant a brute-force penance: re‑embed everything, a costly, time-consuming slog. Or you tolerate a noisy, multi-dialect hybrid, a compromise that eats at performance.

Vec2Vec offers a third way: translation. The ability to shift your vectors into a new space without ever touching the source text.

But beyond this convenience lies a darker truth, a corollary that this paper lays bare: if you can translate, you can exfiltrate. The same magic that offers freedom from lock-in also provides a key for inverting supposedly anonymous vectors, turning a privacy abstraction into a transparent window.

2 The Platonic Representation Hypothesis-Now with Muscles

The paper’s foundations rest on the Platonic Representation Hypothesis-the elegant idea that our menagerie of powerful models aren’t discovering different worlds, but are merely charting different projections of the same underlying semantic universe. The authors don’t just nod to this; they escalate it into a Strong Platonic Representation Hypothesis: this universal geometry is a tangible, learnable, and navigable space. Vec2Vec is their engineered proof, an attempt to build a bridge between the shadows on the cave wall.

3 Vec2Vec in a Nutshell

3.1 Architecture

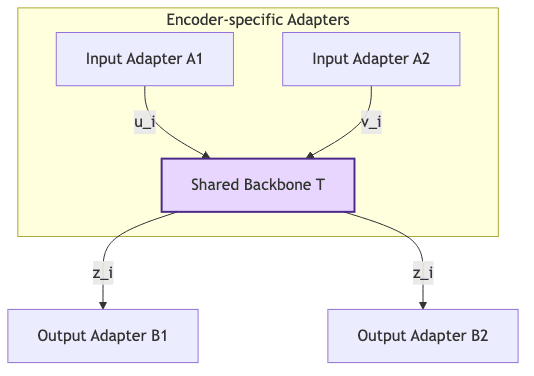
Adapters (𝑨₁, 𝑨₂, 𝑩₁, 𝑩₂) are the gatekeepers: lightweight MLPs that usher raw embeddings to and from the universal backbone.
Backbone T is the lingua franca: a residual MLP operating within the shared, universal coordinate system (dimension Z).

Put together we get translation functions

$F_{1}=B_{2}\circ T\circ A_{1},\qquad F_{2}=B_{1}\circ T\circ A_{2},$

and reconstructions $R_{1},R_{2}$ symmetrical to autoencoders.

3.2 Objective

The training process is not a simple optimization; it’s a carefully refereed adversarial game described by a min–max objective:

$\theta^{*}=\arg\min_{\theta}\;\max_{D}\;\mathcal L_{\textrm{adv}}+\lambda_{\textrm{gen}} \mathcal L_{\textrm{gen}},\tag{1}$

The two core forces in this delicate dance are:

$\mathcal L_{\textrm{adv}}$ : An adversarial pressure cooker. Four distinct GAN losses-two on the raw embeddings, two on the latent space-force the distributions from different models to become indistinguishable.
$\mathcal L_{\textrm{gen}}$ : The geometric anchor. This term combines three critical regularizers:
- Reconstruction loss $\mathcal L_{\textrm{rec}}$ , ensuring the adapters can reverse their own work.
- Cycle‑consistency loss $\mathcal L_{\textrm{CC}}$ , guaranteeing a round trip (e.g., GTE → GTR → GTE) brings a vector back home.
- Vector‑Space‑Preservation loss $\mathcal L_{\textrm{VSP}}$ , the secret sauce, which ensures that local neighborhoods-the relative distances between points-remain intact after translation.

The authors are clear: remove any one of these three generator terms, and the entire structure collapses. The elegance lies in the equilibrium.

4 Results That Matter

Setting	Mean Cosine ↑	Top‑1 Acc ↑	Mean Rank ↓
GTE → GTR (same backbone)	0.75	0.96	1.29
Granite → GTR (cross backbone)	0.80	0.99	1.19
CLIP ↔︎ Granite (multimodal)	0.78	0.35	226

100 = random guess for rank in the 800‑tweet TweetTopic test; lower is better.

Highlights:

The Hypothesis Holds. The translation isn’t just a parlor trick between sibling models. It bridges disparate architectural families-BERT-style and T5-style encoders align with remarkable fidelity. The universal geometry is real.
Robustness in the Wild. Models trained on the clean, structured world of Wikipedia generalize startlingly well to the chaotic syntax of tweets and the specialized jargon of medical records. This isn’t a brittle, over-fitted solution.
A Blaring Privacy Siren. The ability to invert embeddings post-translation is a serious vulnerability. In their tests, up to 80 % of supposedly anonymized Enron emails were partially recovered. Your vector store is less of a black box and more of a translucent one.

5 Playing with Vec2Vec Yourself

Theory is one thing, but truth lives in the execution. The authors provide the tools to get your hands dirty.

# 1. Setup environment (conda recommended)
conda env create -f environment.yml
conda activate vec2vec

# 2. Train a translator (e.g. GTE → GTR) on Natural Questions
python train.py unsupervised_gte_gtr --epochs 3 --num_points 1_000_000

# 3. Translate vectors at inference time
python eval.py --checkpoint checkpoints/gte_to_gtr.pt \
              --source_emb gte \
              --target_emb gtr \
              --input data/dump.npy --output translated.npy

For those who just want to tap into the magic without the training overhead:

from vec2vec.universal import load_translator

gtrify = load_translator("gte_to_gtr")
translated = gtrify(vectors_gte)

6 Strengths & Contributions

The Unsupervised Miracle. No paired data means no need for a parallel corpus, the traditional Rosetta Stone of translation. This is what makes the approach scalable and practical.
Glimmers of a Universal Canvas. The initial success in bridging text and vision (CLIP) hints at a much larger prize: a single, navigable space for all modalities. A true lingua franca for intelligence.
Engineering, Not Alchemy. The project is built on a foundation of solid, reproducible engineering, with configuration-driven experiments. This isn’t a one-off magic trick; it’s a tool.
A Sobering Lesson in Vector Transparency. The paper serves as a critical security reminder: privacy-by-obfuscation in vector space is a fragile promise.

7 Limitations & Open Questions

Limitation	Why it matters
The GAN-Training Gauntlet	The adversarial setup, while powerful, retains its notorious instability. Success still requires patience, multiple restarts, and a feel for hyper‑tuning.
The Curse of Mismatched Dimensions	Translating between spaces of different dimensionality (e.g., CLIP’s 512‑d to a model’s 768‑d) shows reduced fidelity. The VSP loss, in particular, may not scale gracefully to vast dimensional gaps.
The Price of Universality	The reported ≈180 GPU‑days for 36 model pairs is a testament to the computational cost. This isn’t something you’ll run on a single Colab notebook over lunch.
An Empirical Truth, Awaiting its Physics	The Strong Platonic Hypothesis is powerfully demonstrated but remains an empirical observation. The formal, theoretical underpinnings are still an open question.

8 My Read on Future Work

Taming the Beast: Can we replace the volatile GAN framework with more stable contrastive objectives like InfoNCE? This could dramatically improve the training experience.
The Power of a Few Good Examples: If we do have a few paired examples (k ≪ N), could a fine-tuning stage push the translation fidelity past the >0.95 cosine similarity barrier?
Building Defenses: Now that the vulnerability is exposed, can we design defenses? Could a combination of translation and differential privacy create verifiably private shared vector stores?
The Great Chain of Modalities: The ultimate goal is to chain these translators together (text ↔︎ vision ↔︎ audio ↔︎ code) to construct and explore a truly unified semantic manifold.

I’m personally experimenting with a LoRA‑style low‑rank adapter that piggybacks on the published weights-this feels too promising not to probe further.

9 Learn More / Resources

Paper on arXiv: https://arxiv.org/abs/2505.12540
GitHub repo: https://github.com/rjha18/vec2vec
Project page with visuals: https://vec2vec.github.io/
Related unsupervised translation work: Artetxe et al., “Unsupervised NMT 2018”; Liu et al., “MUNIT 2018”.

The geometry is universal. The challenge is building the tools to navigate it. This is a solid step in that direction.

Posted in AI / ML, LLM Advanced by Rakshit Kalra

Harnessing the Universal Geometry of Embeddings – A Vec2Vec Review